Nudged Elastic Band

Published 2025-05-07 • Updated 2025-10-11

The Nudged Elastic Band method uses harmonic biasing to identify the minimum free energy path (MFEP) between images in collective variable space. For this project, I used the two dihedral angles, ϕ and Ψ, of alanine dipeptide; the free energy landscape of ADP is well known, so I was able to compare my results with known literature data. TLDR of results: my implementation provided an accurate MFEP, but had scaling issues, probably because of problems with system initialization.

I used PySAGES, a Python toolkit that overlays enhanced sampling algorithms onto popular molecular dynamics engines, mostly because I worked with their team for some time as an undergrad.

The following is most of a paper I submitted on this for a class, plus some comments.

Introduction/context

Alanine dipeptide is a common system used to model dihedral angles in proteins. Alanine dipeptide has two dihedral angles, ϕ and Ψ, which have different free energies as they describe the conformational state of the molecule. The free energy of a molecule is a crucial quantity in determining the behavior of a system. For example, the free energy determines the three-dimensional structure of proteins, which in turn determines their binding sites and reactivity (1). It is of interest to compute the free energy of alanine dipeptide at various conformational states in order to determine the most stable ones; that is, the (ϕ, Ψ) pairs with the least free energy. It is of even greater interest to compute the minimum free energy path (MFEP) between the two transition states of alanine dipeptide so as to understand the exact conformational change of the molecule. Many simulations have been done on alanine dipeptide, such that there exists a plenitude of literature data on its free energy surface according to its two dihedral angles (2). A challenge with this system, however, is that there exist multiple local minima in the free energy surface, such that the global minimum may be difficult to reach based on the simulation’s starting point (3). A solution to this is to use biased sampling, such as a harmonic bias, to explore regions of low probability density.

The method used here to identify the MFEP of alanine dipeptide is the Nudged Elastic Band (NEB). This method places multiple images along a path between the two transition states of the molecule, then optimizes each image along the free energy surface while keeping the images equidistant to obtain a final curved path between the transition states.

PySAGES takes advantage of the parallel computing power of GPUs to drastically accelerate simulations, through the use of JAX, JIT compilation, and auto-vectorization on the GPU.

Methods

I begin with a pdb file of alanine dipeptide. Notably, this is alanine dipeptide in a vacuum, so it must be initialized to prevent excessive spring forces in the first few iterations. This initialization is done by creating a set of images that form a straight line in CV space between the transition states of interest and using these images as centers in the harmonic biasing algorithm to perform the energy minimization on the alanine dipeptide molecule in the starting pdb file.

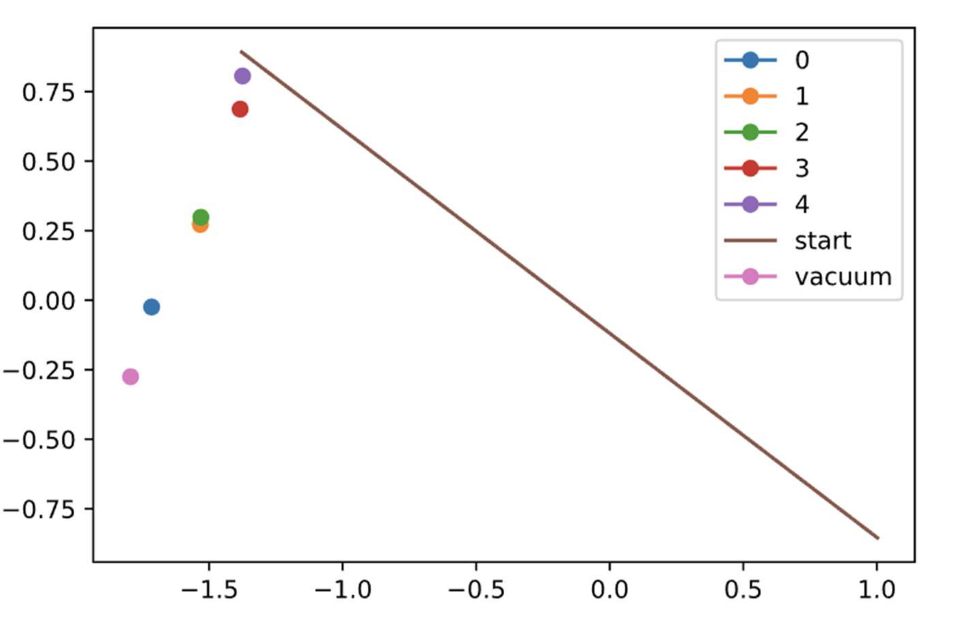
Initial placement of NEB images along the straight-line string between alanine dipeptide transition states. — Initializing NEB images along the linear path between the two transition states.

This image shows the process of nudging an image to where we want it along the starting string (straight line between the transition states of interest). Applying the bias to the vacuum state towards all points along the path yields:

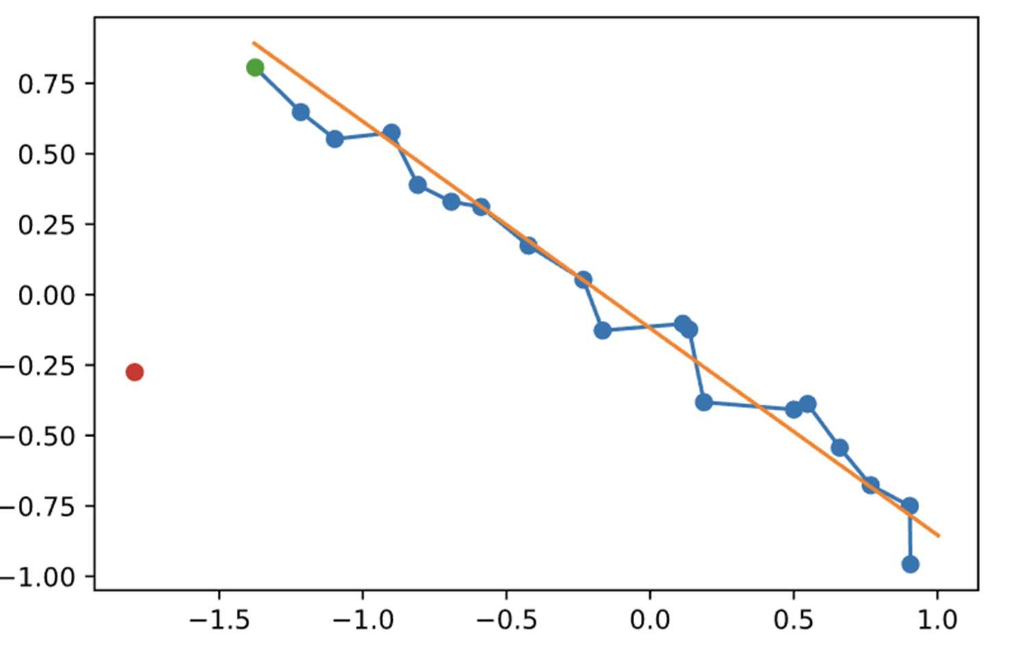
Alanine dipeptide configurations after harmonic biasing along the initial NEB string. — Alanine dipeptide configurations after biasing along the initial string.

Once appropriate pdb files are initialized for all images, iteration 0 may commence. Using the image position as the center, an estimate of the gradient in CV space is obtained using harmonic biasing. The image position is then incremented by this gradient times some constant alpha. To prevent the images from “falling” into free energy basins during the simulation, an adjustment must be made after each iteration to keep the images equidistant along the string. To accomplish this, cubic spline interpolation is first used to identify the functional form of the string in terms of the two collective variables. The algorithm used for this was made multidimensional to allow for any number of collective variables—such that, for future simulations, the NEB method might be easily used for molecules with three or more collective variables—and JAX’s auto-vectoring capabilities were used to accelerate computation for systems with a greater number of dimensions and images along the string. The algorithm produces a matrix of coefficients of the cubic spline which are of the form (4):

$S_i(x)=a_i + b_i\,(x - x_i) + c_i\,(x - x_i)^{2} + d_i\,(x - x_i)^{3}$

These coefficients are found by solving Ax = b, where (note that ai = f(xi), that is, the position of the image):

A = \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots & 0\\ h_{0} & 2\!\bigl(h_{0}+h_{1}\bigr) & h_{1} & 0 & \cdots & 0\\ 0 & h_{1} & 2\!\bigl(h_{1}+h_{2}\bigr) & h_{2} & \cdots & 0\\ 0 & 0 & h_{2} & 2\!\bigl(h_{2}+h_{3}\bigr) & \cdots & 0\\ 0 & 0 & 0 & h_{3} & \ddots\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix}

b = \begin{bmatrix} 0\\[6pt] \dfrac{3}{h_{1}}\bigl(a_{2}-a_{1}\bigr)\;-\;\dfrac{3}{h_{0}}\bigl(a_{1}-a_{0}\bigr)\\ \vdots\\[6pt] \dfrac{3}{h_{n-1}}\bigl(a_{n}-a_{n-1}\bigr)\;-\;\dfrac{3}{h_{\,n-2}}\bigl(a_{n-1}-a_{\,n-2}\bigr)\\[6pt] 0 \end{bmatrix}

x = \begin{bmatrix} c_{0}\\ c_{1}\\ c_{2}\\ \vdots\\ c_{n} \end{bmatrix}

Solving this produces a vector of length n (the number of images) of the third coefficient of the cubic spline. The other coefficients are in terms of a_i and c_i:

d_i = \frac{c_{i+1} - c_i}{3h_i}

b_i = \frac{1}{h_i}\left(a_{i+1} - a_i\right) \;-\; \frac{h_i}{3}\left(2c_i + c_{i+1}\right)

I also used the “not-a-knot” version of the cubic spline rather than the “natural” version to ensure third-derivative continuity of the images at the endpoints of the string.

Cubic spline interpolation illustrating the smooth string used to keep NEB images equidistant. — Testing the cubic splines on a random set of points.

Nicely differentiable, yay.

The derivative of the cubic spline was computed by simple power rule to produce a second matrix, this time of derivative coefficients. At each iteration of the NEB, once a new position in CV space has been calculated for each image, the algorithm is run to obtain a new set of coefficients and derivative coefficients. For each image, the position is then updated by incrementing it by the unit vector (multiplied by some alpha) of the perpendicular component of the string at that point. This ensures that images remain equidistant along the string, while providing some flexibility with this alpha term, which will be further explored in the section below.

Results

To obtain optimal values of alpha and k, NEB was run for a set number of iterations using different pairs of alpha and k:

Comparison of NEB trajectories for multiple combinations of alpha and spring constant k. — Parameter sweep for alpha and k when tuning NEB dynamics.

(plotting ϕ along the x-axis and Ψ along the y-axis)

Based on the above plots, k=70 and alpha=0.2 were chosen to be ideal. This selection was made by a subjective decision of which plots demonstrated best equilibration (yeah it would have been nice to come up with something a little more rigorous here). Finally, the run was performed using the above k and alpha.

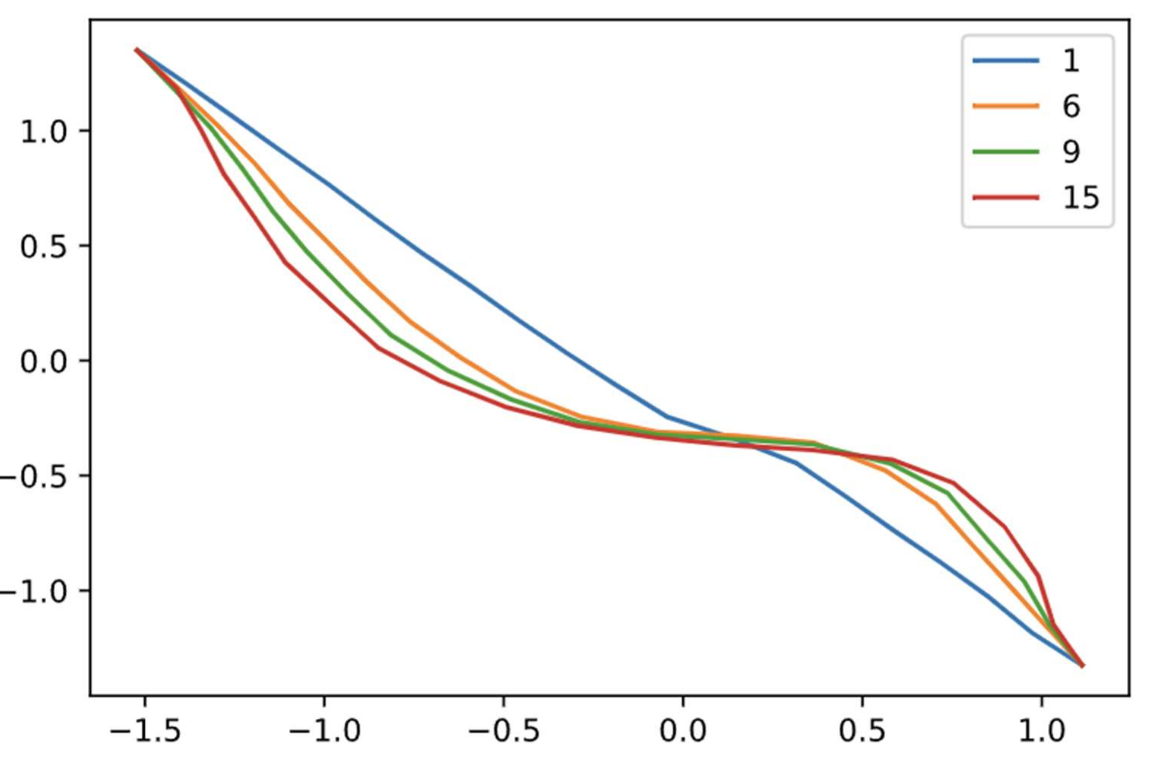
Final minimum free energy path produced by my NEB implementation. — Final MFEP produced by the NEB implementation.

Final run with iteration numbers; I really was not labeling my axes I guess.

There were some issues with maintaining equidistant spacing between images, despite the above algorithm based on cubic splines. For future simulations, it may be beneficial to maintain equal spacing by computing the arclength of the cubic spline between all images, then dividing that length equally.

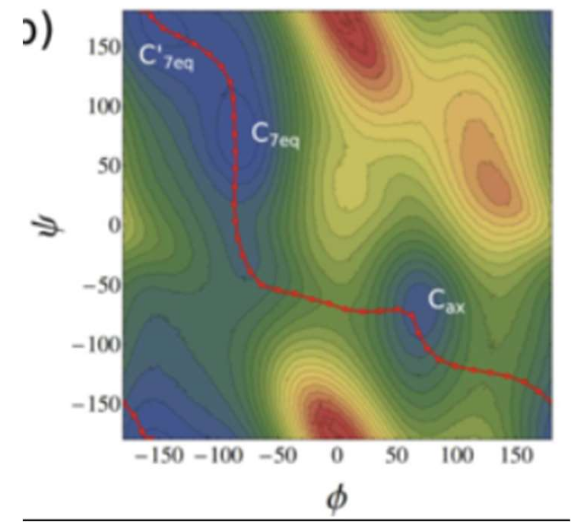
Reference minimum free energy path from Perkett's string method. — Reference MFEP from Perkett for comparison.

From the reference plot above (5), it appears as though the general shape of the MFEP is similar, though there are obvious differences. It is worth noting that the minimum energy basins differ by as much as 17% in CV space, suggesting that the pdb files may not have been well initialized. Finally, an improvement might be to use a climbing image, in which the image with the highest energy after a low number of iterations is driven to the saddle point by inverting the increment, such that it is incremented proportionally to the positive gradient rather than the negative gradient.

Conclusions

The purpose of this simulation was to obtain an MFEP of alanine dipeptide in CV space of (ϕ, Ψ) directly from a starting pdb file of alanine dipeptide in vacuum. This was accomplished using the Nudged Elastic Band method, with which a certain number of images is optimized along the MFEP using harmonic biasing to estimate the negative gradient (or force) in free energy space. The resulting path broadly followed reference data; discrepancies were likely due to difficulties initializing the pdb files and/or keeping the images equidistant. The latter may be remedied by computing the arclengths of the N-1 cubic splines and dividing the images equally along this arclength. For future simulations, it may be of interest to compute a climbing image to obtain the saddle point.

Citations

Moradi, M.; Babin, V.; Roland, C.; Sagui, C. The Adaptively Biased Molecular Dynamics Method Revisited: New Capabilities and an Application. Journal of Physics: Conference Series 2015, 640, 012020. -DOI:10.1088/1742-6596/640/1/012020.
Feig, M. Is Alanine Dipeptide a Good Model for Representing the Torsional Preferences of Protein Backbones? Journal of Chemical Theory and Computation 2008, 4 (9), 1555–DOI:10.1021/ct800153n.
Mironov, V.; Alexeev, Y.; Mulligan, V. K.; Fedorov, D. G. A Systematic Study of Minima in Alanine Dipeptide. Journal of Computational Chemistry 2018, 40 (2), 297–DOI:10.1002/jcc.25589.
Keesling, J. University of Florida. https://people.clas.ufl.edu/kees/files/CubicSplines.pdf
Perkett, M. The String Method. https://sites.google.com/site/mattperkett/research/string